A probability exercise: 2 games down, do the Celtics really have an even chance to prevail over the Knicks?
Today, a little sports math.
The current reigning NBA champion Boston Celtics, owner of a dominant 61-21 record in the regular season, are in a second-round playoff series against the 51-31 New York Knicks. The Celtics were heavily favored to win this series, in part because they won four decisive games against the Knicks during the season.
But in the first two games of the series in Boston, the Knicks prevailed — once in overtime, and once by one point in regulation. In both cases, Boston had opened up a 20-point lead, only to have the Knicks come roaring back amid a rain of missed long-range three-point shots by the Celtics. Now the Knicks have a 2-0 lead in the seven-game series. To win the series, the Celtics must win four of the next five games.
But surprisingly to my sense of probability, oddsmakers are currently giving the Celtics approximately an even chance to win the series.
How unlikely is that?
It’s a fairly straightforward exercise in probability to compute the odds here. I’m going to ignore all the information about who’s injured, who’s got home-court advantage, who’s got a mental edge, and so on. Assuming there is a probability x that the Celtics win each game, what is the likelihood that they’ll win the series? (By the way, the same math now applies to the series between the Cleveland Cavaliers and the Indiana Pacers, where, as with the Celtics, the heavily favored team lost the first two home games of the series.)
For the Celtics to win the series, one of two things must happen.
- They must win the next four games in a row. Probability, x4. Or,
- They must win four games and lose one. Since there are four ways to do that (lose the third game, lose the fourth game, lose the fifth game, or lose the sixth game). Fore each of those scenarios, the probability is x4(1-x) (that is, probability of 4 Celtics wins and one Celtics loss). Since there are four such scenarios, the total probability is 4x4(1-x).
Adding the two, if the Celtics have x chance of winning each game, their chance of winning the series is x4+4x4(1-x). Simplifying, that is 5x4-4x5.
If we assume that the Celtics have an even chance to win each of the remaining games, this means their chance of winning the series is 5(0.5)4-4(0.5)5, or only 18%. That’s pretty unlikely. It’s quite hard to win four out of five after losing two games. (Out of 453 NBA playoff series where a team started 0-2, only 7% came back to win the series.)
But let’s assume the oddsmakers are right. If the Celtics really do have an even chance to win the series now, what does that mean about their chances to win every game?
To figure that out, you must solve the equation 5x4-4x5=0.5. You can’t solve that using algebra, but using graphing or numerical methods, the solution is approximately x=0.69. In other words, for the Celtics to win the series, they need to have a 69% chance of winning each game. Only a huge optimist would believe that after the beating the Celtics took in the first two games. The chart below show all of this graphically. (It’s the same chart for the Cavaliers beating the Pacers, if that’s the series you care about.)
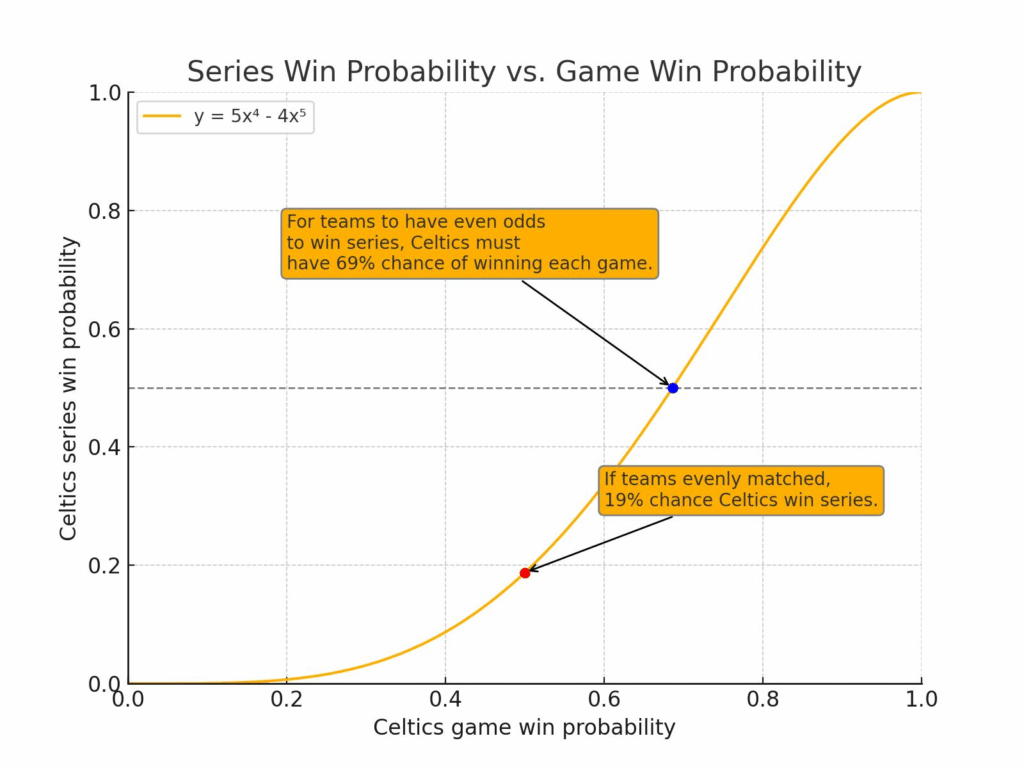
What will happen?
Don’t use this chart to do any betting, please. Remember, I ignored all the factors that the wise guys know all about, like Jason Tatum’s mental toughness, Kristaps Porziņģis’s respiratory illness, Sam Hauser’s ankle sprain, Jalen Brunson’s determination, and thousands of cheering Knicks fans in New York.
But it does give a clear idea of just how big a hole the Celtics have dug for themselves.

I love this.
Oddmakers are, of course, not predicting who will win, but how to even the betting.
It is similar math, but not situation, as in insurance, where the money is to be made elsewhere. In betting, the vigorish is the money-maker; in insurance the ratio is optimal at 1 and the money is made on the float, the money insurance borrows and invests before having to pay it back. I wonder if bookies invest?
I found it interesting that Google search AI was able to confirm that ~0.69 was correct, but unable to solve for x, given just the equation. I would think that this is a perfect question for AI. It is not, because AI sucks.
I recently sent another sports question to Google search and the AI got it wrong. Does the tie go to the runner in baseball? This is an interesting question if you know the baseball rules, the umps, and binary logic. The old saying that the tie goes to the runner is true.