Irrational arguments
Let’s use a mathematical proof to understand the irrational, irrelevant, and distracting ways that people argue these days.
Proof that the square root of two is irrational
If you are math-phobic, be assured that the argument below is relatively painless. You might even enjoy it.
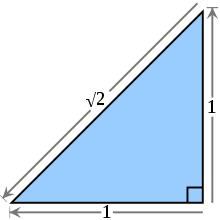
The square root of 2, which we write as √2, is the positive number that when multiplied by itself equals 2. This is an actual quantity. For example, consider a square with sides one inch long. The length of the diagonal (according to the Pythagorean Theorem) is √2 inches.
We can estimate that √2 is slightly more than 1.4 (because 1.42 = 1.4 × 1.4 = 1.96).
The square root of two mystified ancient Greek mathematicians like Plato because they couldn’t nail it down to a number in the class of numbers they considered part of the perfect mathematics of nature, that is, rational numbers.
What is a rational number? It’s simply a number that can be written as a whole number, a fraction (ratio), or decimal. For example, 712, 1/3, 1.4, and 10/7 are all rational numbers. But Plato and his contemporaries could not find a rational number that was equal to √2.
Eventually, they proved there could be no rational number equal to √2. That meant that √2 was an irrational number — outside of the normal scope of ancient Greek mathematics.
Let’s see a classic proof that √2 cannot be rational.
Let’s start by assuming that √2 is some rational number and see what happens. If √2 is rational, it has to equal some fraction. Let’s call that fraction p/q, with an unknown numerator we’ll call p and an unknown denominator of q. Both p and q are whole numbers. If the fraction p/q is not in lowest terms (that is, if p and q have a common factor), we can easily reduce it to lowest terms, so we may as well assume that it is in lowest terms.
Now we do some simple algebra.
√2 = p/q
Multiply both sides by q:
√2 x q = p/q x q = p
Square both sides of the equation √2 x q = p
Left side squared is (√2 x q)2 = √2 x q x √2 x q = √22 x q2 = 2 x q2, because √22= 2.
Right side squared is p2
Since the two side are still equal:
2 x q2 = p2
This means p2 is an even number (a multiple of 2), so p has to be even (the square of an odd number is odd). So p = 2 x r for some whole number r. So we can write:
2 x q2 = (2 x r)2 = 2 x r x 2 x r = 4 x r2
Now divide both sides by 2 and you get:
q2 = 2 x r2
Just as before, this tells you that q has to be even.
But wait a minute. We just figured out that both p and q are even. And that’s impossible, because that means p/q, the fraction we started with, is not in lowest terms, and we started by assuming it was in lowest terms.
So something must be wrong. All the steps we took are valid. The only assumption we made is that √2 is a fraction in lowest terms. So that must be the error. There is no fraction in lowest terms that equals √2. Therefore √2 is not rational. It is a number that cannot be represented as a fraction. It must be irrational.
This method — assuming the opposite of what you want to prove, and then reasoning to a contradiction, which tells you that the original assumption must be false, is called reductio ad absurdum — that is, reducing the assumption to something clearly absurd.
What does this have to do with political discourse?
There are legitimate ways to criticize a logical argument. You can challenge the definitions. You can show that there is a hidden assumption. You can demonstrate that the reasoning is flawed. Because I was trained as a mathematician and worked for 20 years as an analyst, these are the kinds of arguments and challenges I found most satisfying. They bring an intellectual rigor to arguments from evidence.
Unfortunately, that’s not what usually happens in the sphere of political arguments, whether on cable TV or in the comment section of your local news outlet.
Just for fun, let’s imagine what would happen if people brought those types of logically fallacious arguments to mathematics. Can you identify the logical fallacy in each of the following “counterarguments” to my proof?
- You’re wrong. Look at √4. That’s 2. And that’s rational. So is √25. Square roots are rational, obviously.
- Ah. I can see where you are going with this. First you introduce irrational numbers. Then you’ll create some imaginary number that is equal to √-1, when everyone knows you can’t square a number and get a negative answer. Next thing you’ll be introducing quaternions and telling me multiplying things in different orders gives different answers. You’re a force for chaos, and I’m not going to listen to you.
- The distinction between rational and irrational is rooted in Eurocentric white people’s thinking. In a multicultural 21st century context, why are we still drawing these unfair comparisons?
- Let’s go back to root causes. The question is not whether √2 is irrational. The question is, what made us think it had a fighting chance to be rational in the first place? After everything that we put its ancestors through, from the Sieve of Eratosthenes to the Serpinski Gasket, it’s a wonder that √2 is a number at all, regardless of how irrational. Let’s not condemn it for its irrationality. Let’s get it appropriate treatment so it can have some sort of a life that approaches rationality.
- There are plenty of rational numbers close to √2. Take 10/7. Square it and you get 100/49, which might as well be 2. If you can get that close, why quibble over the last few decimal places?
- You said that your numbers p, q, and r are either even or odd. That’s binary thinking. Perhaps they can be even sometimes and odd other times. Then your argument falls apart.
- Forget all this symbol manipulation. Get a block of wood one inch on a side. Now saw it in half along the diagonal. Then measure the length of the diagonal. Whatever you measure, that’s √2. It’s a number right there on your ruler. So you must be wrong.
- You’re assuming numbers don’t change. Perhaps that was true in the past, but in 2022, we need to account for inflation. √2 is likely now 5% or 10% larger than it was at the start of the year, growing every month, depending on the mathematical supply chain. And somewhere in there, it must surely have grown enough to be a normal rational number.
- Mathematicians defined square roots and rational numbers. And you’re a former mathematician. This argument just reinforces your own biases. Why should us real-world people that live regular real-world lives even accept arguments from within your mathematician echo-chamber ivory tower?
- Truth is not a concept that has any validity in current discourse. Have you ever heard of alternative facts? Surely there are those who believe that √2 is a rational number — who are you to invalidate their beliefs? Denying their reality makes you part of cancel culture.
- Until you can prove there is no fraud in the way you manipulate numbers, we have to treat the results you come up with as illegitimate, even if the mathematical equivalent of the Electoral College says otherwise.
- You say that reaching an absurd conclusion proves your original assumption was wrong. But politicians reach absurd conclusions all the time. Absurd conclusions are integral to our democracy. So you can’t de facto rule out any absurd conclusion and use it to prove anything.
- This backlash against rationality began with Barack Obama, who was far too dedicated to logic and out of touch with what the majority of Americans wanted. Irrationality is now a completely valid political position, whether we’re talking √2 or whether the president sets oil prices.
- I’m going to point a gun at your head until you agree that √2 is just as rational as any other number. Ha, got you now!
There is nothing elitist in requiring those you deal with to state their assumptions, make rigorous arguments, gather research to back them up, and defend their positions against normal, logical counterexamples.
Math has taught us something. Let’s not lose it in the lunacy that passes for discourse.
You promised there would be no math…
I guess “no math” was an irrational expectation. 🙂