When pie charts don’t total 100%

Consider the pie chart shown below, for a survey of grocery shoppers who were asked “What is your favorite fruit?” and given four choices: apples, bananas, cherries, or dates. Is something wrong here?

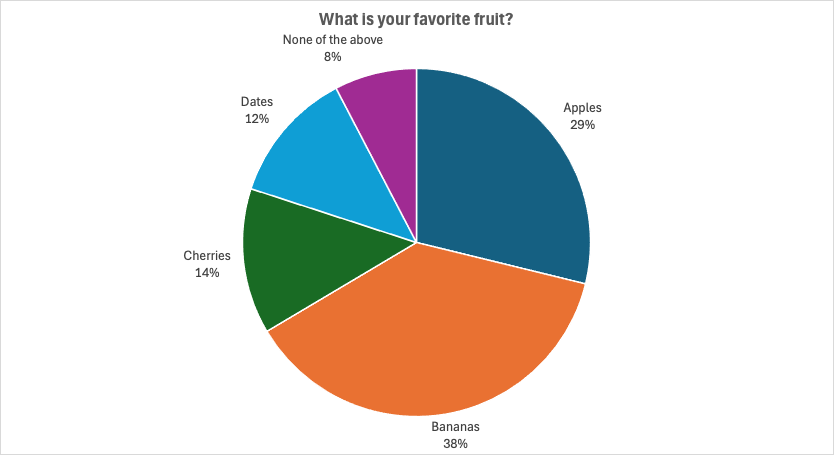
Pie charts are supposed to add up to 100%. But the percentages here add up to 101%. Clearly the people collecting and displaying the data made an error, right?

Unfortunately, as anyone whose ever done a survey knows, it’s not that simple. Below you can see the underlying data for the (hypothetical) survey shown in the chart, which reached 170 shoppers out of the 5,000 regular customers at the supermarket:

Favorite Fruit Survey	Responses	Percent (rounded)	Percent (3 decimals)
Apples	49	29%	28.824%
Bananas	64	38%	37.647%
Cherries	23	14%	13.529%
Dates	21	12%	12.353%
None of the above	13	8%	7.647%

Now you can see why there is a problem. Four of the five percentages were rounded up. This causes the total to increase beyond 100%.

Three solutions to this data display problem

Here are three options for displaying this pie chart that address the “doesn’t add to 100%” problem. When I posed this problem to my followers on LinkedIn, several selected one of the first two options, which, as I’ll explain, are both problematic.

1. Alter one of the numbers to make the total 100%. In this case, we could change “Cherries” to 13%, and it would still be close to accurate — and the numbers would add to 100%. But there is no justification for changing data here except to make everything nice and neat. Editing data to make it look better by rounding numbers greater than 0.5 down are a form of deception, since it does not accurately reflect reality or the expected rules of rounding.
2. Show more decimal places. If you round to one decimal place, perhaps you can eliminate the problem. In this case, the percentages rounded to one decimal place are 28.8%, 37.6%, 13.5%, 12.4%, and 7.6%. And that totals to . . . 99.9%. We haven’t eliminated the problem of failing to sum to 100%, we’ve just pushed it off one decimal place. Worse yet, we have indicated that our numbers reflect an inappropriate amount of accuracy. According to the calculator at SurveyMonkey, if this sample of 170 people is supposed to represent 5000 shoppers, the margin of error for the sample is 7%. Posting a number like 28.8% implies a margin of error in the tenths of a percent. While it might seem like 28.8% is more accurate, it’s promising an accuracy that the sample does not support. (A sample of 3000 would have a margin of error of less than 1%; in that case, you could show the tenths of a percent in the pie chart.)
3. Include a note that says “Percentages may not total 100% due to rounding.” While this is correct, it’s inelegant. Still, in a case like this, it is the right thing to do.

Could we dispense with the note?

I’ve fielded hundreds of surveys and posted thousands of results — in fact, I originated the multi-million-dollar survey business called Technographics at Forrester Research. With all that experience, I thought I knew the right answer: trust people to understand that rounded numbers don’t always add up to the exact total you would expect.(In fact, any pie chart data display in which there are more than two answers and the number of responses is not a multiple of 100 is subject to the same rounding issue.)

Sadly, my confidence in the statistical sophistication of my followers was misplaced. The purpose of my LinkedIn post was to conduct a poll to determine if people just “get” this. And unfortunately, they don’t.

I gave an example of a pie chart that added up to 101%, and asked which explanation would be most likely. Out of 58 responses to my post, 53 selected “Total > 100% due to rounding.” But 5 respondents (9% of the total) selected “The pie chart must be in error.” Some of my followers said that the pie chart not adding up to 100% was “sloppy” or showed a lack of proofreading. And some attempted to “fix” it with the inappropriate solutions described earlier.

You might expect my followers to be more sophisticated than the average user, since I worked for a research company that frequently posted statistics from surveys. Nope, they still were confused. I’m sure that among more general audiences, the number who would call a pie chart that doesn’t add up to 100% erroneous would be even higher.

So I learned my lesson. We have to include a note about rounding, even though most of the audience likely knows that already.

Just don’t try to make me fudge the numbers or add inappropriate levels of precision just to feed your sense of neatness. Truth in data is more important than neatness. And that’s a hill I’ll die on.