Elections, hurricanes, and the uncertainty conundrum
I have two simple questions for you.
Is Elizabeth Warren the most likely democratic candidate to win the Democratic nomination?
Is Elizabeth Warren more likely than not to win the Democratic nomination?
One way to analyze these questions is to look at the odds on a site like PredictIt. As I write this, you can buy a bet on Warren to win the nomination for 33 cents. It costs 68 cents to bet against her. This implies that she has about a one in three chance to win.
On the other hand, her position is better than Joe Biden (26 cents to win), Bernie Sanders (15 cents), or Kamala Harris (13 cents). They’re each more of a long shot than Warren is.
So Warren is most likely to win, but there’s a greater chance that she’ll lose than win. The most likely to win (Warren) is not the likeliest outcome (Warren loses).
While this makes logical sense, it confuses the brain. We want a predicted winner. People who say Warren is the front-runner by this calculation will get savaged as poor predictors — even though if they’d chosen anyone else, their prediction would be even less likely to come true.
What does this have to do with hurricanes?
Take a look at this map, accurate as of Monday morning, of where hurricane Dorian is headed.
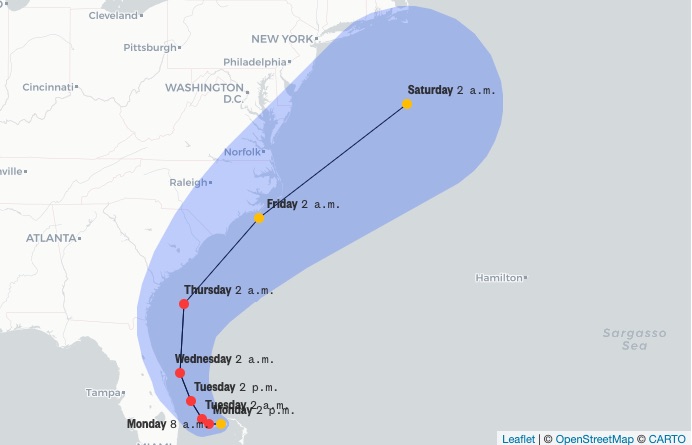
Now answer this question: will the center of the storm hit Florida?
The red dots indicate a major hurricane, and the path is clearly going northward, up the coast, and not westward, towards Florida. Wow, that was close.
But wait a minute. What is the blue-grey shading? That’s not the width of the storm. It’s the uncertainty. If it’s about the same as described in this excellent New York Times interactive opinion piece, it’s the area that has about a two-thirds chance of including the center of the storm. (That means there’s about a one-third chance it will go either east or west of the shaded area.)
Is the center of the storm going to hit Florida? Given that that most of the shaded area is outside Florida, the answer is, it’s more likely than not that it will miss Florida.
On the other hand, the shaded area represents the area of likeliest paths. And some of those paths hit Florida.
So a forecaster could, in good conscience say both, “There is a fair likelihood the storm will make landfall in Florida” and, “It is more likely than not that the storm will miss Florida.”
Just as with Elizabeth Warren, the most likely path is not the likeliest outcome. In fact, it’s likely that the storm will go somewhere other than on that neat, northward path that’s causing everyone in Florida to feel as if they dodged a bullet.
I hope it misses Florida, but it’s too soon to say, just as it is too soon to predict who the Democratic nominee for president is.
I can predict that if you live in Florida, you’re going to see a hell of storm, I’m just not sure how strong . . . and nobody else is, either.
Partial information confuses
We want to know who will win. We want to know where the storm will hit. Modern statistical theory provides us with information on those outcomes, but not certainty. As humans, we’re not good at reasoning with uncertainty.
This causes people to jump right to the conclusions (Warren will win, the storm will miss Florida) as soon as there is statistical information available. This is an error. Even after the surprising outcome of the 2016 election, when an event Nate Silver predicted as about a one-in-three chance occurred, we will blame the forecasters and not our own inability to intuitively grasp uncertainty.
This is not curable. It’s human nature.
What is curable is to learn about logic. Don’t give in to your desire for certainty. Recognize that until there is more information, predictions are uncertain, and cases like these, the most likely path is not the likeliest outcome.
Preparing for less likely outcomes is how you hedge in these situations. That means you can’t count on Warren winning, and you can’t count on Florida escaping Dorian. So prepare for other outcomes, even if those are not the most likely.
Your nature wants you not to do this. Fight it. Because math has no pity.